Factorisation d’un Polynôme
sous forme de
cours et d’un exemple de base
Théorème : Factorisation d’un polynôme
On peut mettre x – a en facteur dans un polynôme si est seulement si
a est une racine du polynôme.
Etudions
la fonction f ( x ) = x3
- 3 x - 2
Je cherche les racines évidentes : x = 2 est une racine évidente car f ( 2 )
= 23 – 3 . 2² - 2 = 8 – 6 – 2 = 0
PS/ Une racine évidente est une solution comme -2, -1, 0, 1, 2
D’après le théorème annonce précédemment, on peut mettre x – a
en facteur :
1 er méthode : Par
identification
f ( x ) = ( x – 2 ) ( polynôme de degré 2 ) soit
f ( x ) = ( x – 2 ) ( a x2 + b x + c )
PS / A cette étape, le polynôme doit avoir tous ses termes
positifs.
Développons : f ( x
) = ( x – 2 ) ( a x2 + b x + c ) = a x3 + b x² + c x – 2
a x² - 2 b x – 2 c
 f
( x ) = a x3 + ( b
-2a ) x² + ( c – 2b ) x - 2c
f
( x ) = a x3 + ( b
-2a ) x² + ( c – 2b ) x - 2c
{

a = 1 → a = 1
b
-2a = 0 → b
= 2
c –
2b = -3 → c
= 1
-
2c = - 2 → vérification
: c = 1
Nous retenons : f ( x ) = ( x – 2 ) ( x2 +
2 x + 1 )
Etudions
de nouveau la fonction f ( x ) = ( x – 2 ) ( x2 + 2 x + 1 ) est
essentiellement
f1 (
x ) = x2 + 2 x + 1
Je cherche les racines évidentes : x = - 1 est une racine évidente car f1 ( - 1 ) = ( - 1 )2
+ 2 . ( - 1 ) + 1 = 0
Développons : f1 ( x
) = ( x + 1 ) ( a x + b ) = a x² + b x + a x + b = a x² + ( b + a ) x + b
{
a =
1 → a = 1
b +
a = 2 → b = 1
b =
1 → vérification
: b = 1
Nous retenons : f2 ( x ) = ( x + 1 ) ( x
+ 1 )
Conclusion :
f ( x ) = ( x – 2 ) (
x + 1 ) ( x + 1 )
Etudions
la fonction f ( x ) = x3
- 3 x - 2
2 er méthode : Par
division
Je cherche les racines évidentes : x = 2 est une racine évidente car f ( 2 ) = 23 – 3
. 2² - 2 = 8 – 6 – 2 = 0
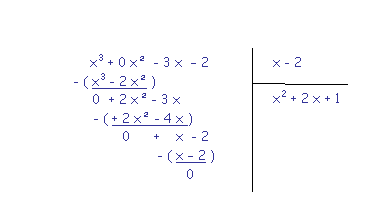
Nous retenons : f ( x ) = ( x – 2 ) ( x2 +
2 x + 1 )
Etudions
de nouveau la fonction f ( x ) = ( x – 2 ) ( x2 + 2 x + 1 ) est
essentiellement
f1 (
x ) = x2 + 2 x + 1
Je cherche les racines évidentes : x = - 1 est une racine évidente car f1 ( - 1 ) = ( - 1 )2
+ 2 . ( - 1 ) + 1 = 0
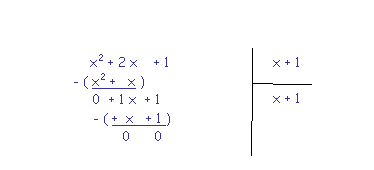
Conclusion :
f ( x ) = ( x – 2 ) (
x + 1 ) ( x + 1 )